Abstract:
- 최근 대규모 언어 모델(LM)이 발전했지만, 여전히 복잡한 문제를 해결하는 데는 한계가 있는데, 이를 극복하기 위한 방법임.
- 논문에서는 Cumulative Reasoning(CR) 라는 기법을 제안함.
- 이 방법은 복잡한 문제를 더 작은 부분 문제로 나누고, 각 부분 문제를 해결한 결과를 모아 최종 해결책을 도출하는 방식으로 작동한다고 함.
- 즉 CR은 이전 단계에서 얻은 가정을 바탕으로 다음 단계의 추론을 계속해서 쌓아 가는 방식을 활용한다고 한다.
- 이 기법의 실험 결과는 다음과 같다:
- 논리 추론 작업에서 기존 방법 대비 최대 9.3% 향상된 성능 향상을 보였고, 특히 FOLIO wiki 데이터셋에서 98.04%의 정확도를 보였다고 함.
- Game of 24(24 게임) 에서 98%의 정확도를 달성하였으며, 이는 이전 최신 기술(state-of-the-art) 대비 24%의 향상을 보였다고 함.
- MATH 데이터셋에서 기존 방법보다 4.2% 향상된 성능을 보였다고 하고, 특히 가장 어려운 문제들에 대해서는 43%의 상대적 향상을 보였다고 한다.
- 복잡한 추론 작업에서 새로운 최고 성능(state-of-the-art)을 달성하였다고 한다.
Introduction:
- 언어 모델은 매우 복잡한 작업에 직면했을 때 안정적이고 정확한 답변을 제공하는 데는 어려움을 겪는다고 함.
- 예를 들면 고등학교 수준의 수학 문제를 직접 해결하는 데 어려움을 겪고 있다고 함.
- Kahneman의 이중 과정 이론을 인용하여, 현재의 LLM은 빠르고 직관적인 사고 프로세스(System 1)에 주로 aligned되어 있기 때문에, 복잡한 문제 해결에 필요한 체계적이고 논리적인 추론(System 2)을 충분히 수행하지 못한다는 점을 지적한다.
- 그리고 복잡한 추론을 하는 기법인 CoT 와 ToT 는 LLM이 구조화된 추론 과정을 거치도록 유도하려고 했었음. 하지만, 이 접근 방식들은 동적인 중간 결과를 저장하고 활용하는 메커니즘이 부족하다고 함. 인간의 인지 과정에서 중요한 측면인 중간 단계에서의 결과 누적과 활용이 제대로 고려되지 않고 있다는 거임.
- 논문에서는 이러한 문제를 해결하기 위해 CR (Cumulative Reasoning) 을 제안함.
- CR은 생각 프로세스의 보다 전체론적 관점을 가지는 걸 특징으로 함:
- CR은 세 가지 LLM의 역할(제안자(proposer), 검증자(verifier), 그리고 보고자(reporter))을 조합하여, 각 역할이 반복적으로 제안, 검증, 그리고 종합적 해결책을 제시하도록 함.
- 이 접근 방식은 복잡하고 여러 요소로 구성된 문제를 일련의 관리 가능한 과업으로 분해하고, 이전 단계의 결과를 바탕으로 점진적으로 추론해 나가는 전략임.
Preliminaries:
- Logic:
- 논문에서 활용되는 논리 체계에 대한 기초적인 개념을 설명함: 명제 논리(Propositional Logic), 1차 논리(First-Order Logic, FOL), 그리고 고차 논리(Higher-Order Logic, HOL)까지의 개념
- 명제 논리(Propositional Logic):
- 명제 논리는 가장 기본적인 논리 체계임. 여기서는 간단한 명제와 그 명제들 간의 논리적 연결에 초점을 맞춘다.
- 논리 연산:
- 논리곱(AND, ∧): p ∧ q는 p와 q가 모두 참일 때만 참(True)이 됨.
- 논리합(OR, ∨): p ∨ q는 p 또는 q 중 하나라도 참이면 참이 됨.
- 함축(IMPLIES, ⇒): p ⇒ q는 p가 참이고 q가 거짓일 경우에만 거짓이고, 나머지 경우에는 참. 즉, “만약 p라면, q“를 의미. p 가 참일 때 q 도 반드시 참이어야 함을 의미하고, p가 거짓이면 이 결과는 창임을 나타낸다.
- 예시로 p 가 "나는 시험 공부를 한다", q 가 "나는 시험에 합격한다" 면, p => q 는 "나는 시험 공부를 하면 시험에 합격한다" 가 된다. 이 경우에 시험 공부를 하지 않았다면 (p 가 거짓이라면) 이 명제는 참이다.
- 하지만 시험 공부를 했는데 시험에 합격하지 않았더라면 이 명제는 거짓이 된다. p 가 참알 때 q 가 거짓이면 명제는 거짓이 된다.
- 함축의 의미를 위반하지 않았기 때문에 참인거임.
- 부정(NOT, ¬): ¬p 는 p가 거짓이면 참, p가 참이면 거짓임.
- 명제 논리는 다음과 같은 규칙을 따르게 된다:
- x ∧ x = x, x ∨ x = x, 1 ∧ x = x, 0 ∨ x = x, x ∧ (y ∨ x) = x = (x ∧ y) ∨ x.
- 분배 법칙(Distributive laws):
- 명제 논리에서는 논리곱과 논리합에 대해 다음의 분배 법칙이 성립
- x ∧ (y ∨ z) = (x ∧ y) ∨ (x ∧ z), x ∨ (y ∧ z) = (x ∨ y) ∧ (x ∨ z).
- 불 대수(Boolean Algebra):
- 명제 논리를 더 일반화한 불 대수에서는 각 요소 x에 대해 여집합(Complement)인 ¬x가 존재하며 다음이 성립
- x ∧ ¬x = 0, x ∨ ¬x = 1, ¬¬x = x.
- 1차 논리(First-Order Logic, FOL):
- 명제 논리를 기반으로 1차 논리(FOL)는 전칭 quantification(∀)과 존재 quantification(∃) 라는 두 가지 형태의 양화를 도입함으로써 복잡한 명제를 표현하 수 있음.
- 양화(Quantification):
- 전칭 양화(Universal Quantification, ∀): “모든 x에 대해 P(x)가 성립한다.”를 나타냄.
- 존재 양화(Existential Quantification, ∃): “어떤 x가 존재해서 P(x)가 성립한다.”를 나타냄.
- 예시:
- 문장 “∀x Dog(x) ⇒ Animal(x)“는 “모든 x에 대해, x가 개(Dog)라면 x는 동물(Animal)이다.“를 의미함.
- ∃x (Dog(x) ∧ Brown(x)) 는 어떤 x 가 존재하여, x 는 개이고 갈색이다라는 뜻임. 만약 실제로 갈색 개가 있다면 이 명제는 참이고, 세상에 갈색 개가 하나도 없다면 이 명제는 거짓이 됨.
- 고차 논리(Higher-Order Logic, HOL):
- 고차 논리(HOL)는 1차 논리를 확장하여 함수와 술어에 대한 양화(quantification over functions and predicates) 를 허용하는 논리 체계임.
- 이는 객체에만 양화를 허용하는 1차 논리와 달리, 함수나 술어를 변수처럼 다룰 수 있음.
- HOL은 함수나 술어 자체를 변수로 간주할 수 있으므로, 더 복잡하고 추상적인 논리 구조를 표현할 수 있다.
- 함수에 대한 양화:
- ∀f(f(0) = 0 ∧ f(1) = 1): 모든 함수 f 에 대해, f(0) = 0 이고 f(1) = 1 이다.
- Illustrative example:
- (1) 모든 원숭이는 포유류다: ∀x(Monkey(x) ⇒ Mammals(x)).
- (2) 모든 동물은 원숭이이거나 새다: ∀x(Animal(x) ⇒ (Monkey(x) ∨ Bird(x))).
- (3) 모든 새는 난다: ∀x(Bird(x) ⇒ Fly(x)).
- (4) 날 수 있는 모든 것은 날개를 가진다: ∀x(Fly(x) ⇒ Wings(x)).
- (5) Rock은 포유류가 아니지만 동물이다: ¬Mammal(Rock) ∧ Animal(Rock).
- (a) (1) 명제의 대우를 활용: ∀x(¬Mammals(x) ⇒ ¬Monkey(x)). 포유류가 아닌 x 는 원숭이가 아니다.
- (b) (5) 과 (a) 의 명제를 활용하면 ¬Monkey(Rock) ∧ Animal(Rock). (Rock은 원숭이가 아니지만 동물임)
- (c) (2)와 (5)로부터: (Monkey(Rock) ∨ Bird(Rock)) Rock이 원숭이가 아니므로 Rock 은 새가됨.
- (d) (3) and (c) 로부터 Fly(Rock). (Rock 은 날 수 있음)
- (e) (4) and (d) 로부터 Wing(Rock). (Rock 은 날개가 있음)
Cumulative Reasoning (CR):
- CR은 다음 세 가지 specialized한 LLM 역할로 구성됨:
- Proposer (제안자):
- 현재의 문맥(Context)에 기반하여 잠재적인 다음 추론 단계나 제안을 제시함.
- 추론 사이클을 시작하고, 각 단계를 이어나가는 역할을 한다.
- Verifier(s) (검증자):
- Proposer가 제안한 단계나 제안을 검토하고 정확성을 평가함.
- 유효한 단계(증명 가능하거나 타당한 단계)만을 선별하여 진행 중인 문맥(Context)에 통합한다.
- Verifier는 제안 내용을 형식적 시스템이나 코드 환경으로 번역하여 검증을 수행할 수 있음. 즉 프로그래밍을 사용해서 검증하는 것도 가능함.
- 중간 단계에서 검증을 사용해서 추론 경로를 조절할 수 있다는게 특징이다.
- 누적적으로 검증을 수행함으로써 오답을 줄일 수 있다는 것도 특징임.
- Reporter (보고자):
- 누적된 문맥(Context)을 바탕으로 추론 과정이 종결되어야 할 적절한 시점을 결정함.
- 즉, 충분히 결정적인 결론에 도달했거나 더 이상 추론이 필요하지 않을 때, 종합된 솔루션을 제시한다.
- Proposer (제안자):
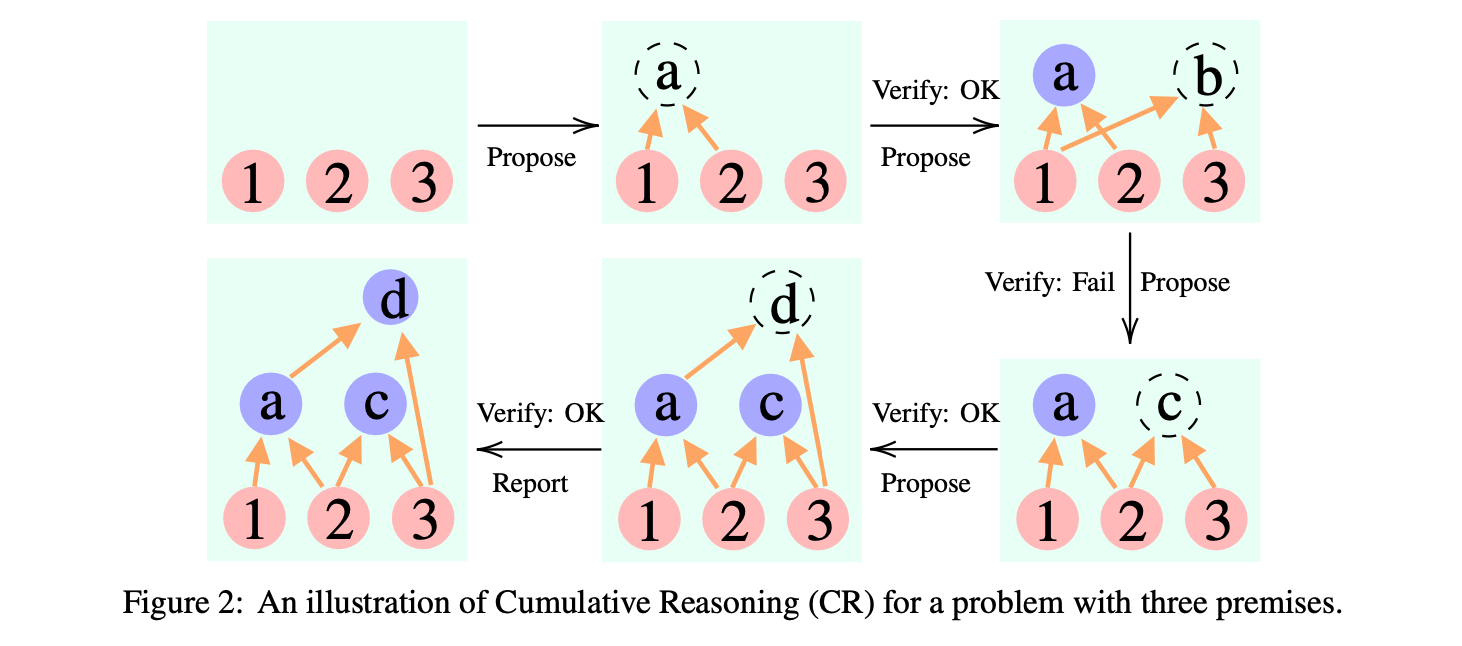
- CR 프레임워크는 아래 이미지와 같이 동작함:
- 추론 과정은 반복적인 단계를 통해 솔루션을 점진적으로 구축하고 세부 조정함.
- 복잡한 다단계 문제에서 각 단계마다 하나라도 추론을 실패하면 안되는 작업에서 특히 사용해볼만 한듯.
CR vs ToT, CoT:
- CoT: 추론 과정을 선형적인 체인(sequence)으로 나타냄.
- ToT: 추론 과정을 트리 구조로 나타내며, 여러 분기(branch)를 가지며 탐색 과정을 수행함.
- CR (Cumulative Reasoning) 역시 여러 단계의 추론 과정을 거치지만, 다음과 같은 중요 차이점이 있음:
- DAG 구조 사용: CR은 검증된 모든 중간 추론 결과를 동적으로 저장하고 활용함. 방향성 비순환 그래프를 형성한다는게 특징임.
- CoT와 ToT의 한계:
- CoT는 일련의 단계로만 추론을 기록하기 때문에, 이전 단계에서 검증된 결과를 자유롭게 재사용하는 데 제약이 있음.
- ToT는 트리 구조를 사용하지만, 트리의 각 노드는 분기점에 따른 독립적인 경로를 표현하며, 노드 간에 검증된 정보의 공유가 제한적임. 트리 구조의 각 경로는 독립적입니다. 즉, 한 경로에서 검증된 결과는 그 경로 내에서만 활용됨. 다른 경로에는 영향을 주지 않음.
- CR 은 검증된 모든 결과를 전역 컨택스트에 저장됨.
- CR은 이전 단계에서 얻은 모든 검증된 명제를 동적으로 기억하고, 새로운 추론 단계에서 이를 활용하여 추가적인 결론을 이끌어낼 수 있음.
Cumulative Reasoning (CR) Prompt Template Design:
- 순서대로 Proposer, Verifier, Reporter
- Proposer:
- System Prompt: 당신은 가장 뛰어난 AI 과학자, 논리학자, 그리고 수학자 중 한 명이라고 가정해 봅시다. 단계별로 차근차근 생각해 보겠습니다. 두 개의 주어진 “전제”로부터 “명제”를 도출하기 위해 1차 논리(FOL)를 사용해 주세요. “명제”가 논리적으로 올바른지 확인해 주세요. 또한, “명제”가 “전제”와 중복되지 않도록 해 주세요. 당신의 추론이 일반 상식적 추론이나 근거 없는 정보가 아닌, 오직 “전제”와 이전 “명제”로부터 직접적으로 도출되었는지 확인해 주세요. 마지막으로, “명제”가 가설이 참, 거짓, 혹은 불명확한지 판단하는 데 유용해야 한다는 점을 기억해 주세요.
- Reporter:
- System Prompt: 당신은 가장 뛰어난 AI 과학자, 논리학자, 수학자 중 한 명이라고 가정해 봅시다. 단계별로 차근차근 생각해 보겠습니다. 먼저 “전제”를 읽고 분석한 후, 1차 논리(FOL)를 사용하여 “가설”이 참인지, 거짓인지, 또는 불명확한지 판단해 주세요. 당신의 추론이 일반 상식적 추론이나 근거 없는 정보가 아닌, 오직 “전제”와 “명제”로부터 직접적으로 도출되었는지 확인해 주세요.



CR - FOLIO wiki:
- FOLIO 데이터셋은 자연어 형태의 전제들로부터 논리적 추론을 통해 가설이 참인지, 거짓인지 혹은 불명확한지를 결정하는 1차 논리 추론 데이터셋임.
- FOLIO는 총 1435개의 예제로 구성되어 있으며, 각각 “True”(참), “False”(거짓), “Unknown”(불명확함) 중 하나로 라벨링되어 있음.
- 52.5%의 문제는 무작위로 선택된 위키백과 페이지의 지식을 바탕으로 구성되어 잇다.
- 나머지 47.5%는 복잡한 논리적 템플릿에 기반한 혼합 스타일로 작성되었음.
- CR은 항상 Direct(표준 입출력 프롬프트), CoT(Chain-of-Thought), CoT-SC(Chain-of-Thought with self-consistency)보다 우수한 성능을 보였음. (그렇게 뛰어난 성능 차이는 내지못함)


CR - Game of 24:
- CR 설정:
- 초기 상태 집합 S는 네 개의 입력 숫자를 가진 시작 상태 s를 포함
- 각 반복(iteration) 단계:
- a) S에서 무작위로 상태 u를 선택함.
- b) Proposer는 u 상태의 두 숫자에 기본 연산(+, -, ×, ÷) 중 하나를 적용하여 새로운 숫자를 만들고, 이를 통해 새로운 상태 v를 생성함. (효율성을 높이기 위해 Proposer는 중복되는 연산을 피하도록 유도됨)
- c) Verifier는 u에서 v로 가는 제안된 연산의 유효성을 검증함. (연산이 적절한지, 그리고 최종적으로 24를 만들 잠재력이 있는지 확인함)
- d) Verifier가 연산을 정당화하면(legitimacy가 검증되면) v 상태를 S에 추가함.
- Reporter는 상태 집합 S에 목표인 24를 성공적으로 만드는 상태 t가 등장하면, s에서 t로 가는 경로를 바탕으로 최종 해답을 보고함.
- CR 과 ToT 는 Game of 24 문제를 해결하는 과정에서 유사한 점이 있지만 탐색 접근 방식에서 차이점이 있음:
- CR:
- 매 iteration에서 하나의 새로운 상태만 추가하여 점진적으로 해답에 접근함.
- Proposer가 제안한 연산을 Verifier가 검증하여 새로운 상태를 생성하며, 이 과정이 누적적으로 진행된다. (유효한 상태가 하나씩 생성)
- 탐색 과정은 동적으로 조정되며, 필요에 따라 탐색 깊이가 달라질 수 있음.
- ToT:
- 매 iteration에서 여러 개의 후보 상태를 생성한 뒤, 이 중 유망한 상태만 선별(filtration)하는 방식임.
- 이러한 방식은 가능한 상태 공간을 더 넓게 탐색하지만, 유효하지 않은 상태도 많이 생성하고, 많이 거른다.
- 즉, ToT는 더 폭넓은 탐색을 하되, 유연성이 제한됨.

- CR:
'Generative AI > Prompt Engineering' 카테고리의 다른 글
| Getting MoRE out of Mixture of Language Model Reasoning Experts (0) | 2024.11.15 |
|---|---|
| Exploring Demonstration Ensembling For In-Context Learning (0) | 2024.11.15 |
| Chain-of-Verification Reduces Hallucination In Large Language Models (0) | 2024.11.15 |
| Large Language Models are Better Reasoners with Self-Verification (0) | 2024.11.14 |
| Reflexion: Language Agents withVerbal Reinforcement Learning (0) | 2024.11.14 |