Abstract:
- 논문의 초록(Abstract)은 대규모 언어 모델(LLM)을 코드 생성(Code Generation) 목적으로 미세 조정(fine-tuning)할 때, 효율적인 데이터 사용 방법을 제안함.
- 그러니까 합성 데이터를 만들어 낼 때 중복이 많이 발생하는데 이를 제거하는 기법에 대해서 다룸.
- 이런 아주 유사하거나 동일한 코드 예제, 혹은 문제 구조가 비슷한 데이터를 무리하게 많이 포함하면, 학습 효율이 떨어지거나 모델 성능 향상에 큰 이점이 없기 때문.
- 여기서 소개하는 데이터 프루닝(Pruning) 기법은 다음과 같음:
- 데이터 프루닝(필요 없는 데이터를 잘라내는) 방법을 사용해 ‘효율’을 높이면서도 ‘성능’을 유지 또는 향상시키는 전략을 제시
- 여러 가지 클러스터링, 다양한 기준(metric) 등을 활용해, “성능에 유의미한 정보를 담지 않는” 데이터 또는 “중복된” 데이터를 뽑아내어 제거함.
- 본 실험에서는 전체 데이터의 10%만 사용해도 벤치마크 성능이 거의 유지됨을 보였다고 함.
- 더 나아가, 적당한 수준의 프루닝은 데이터를 줄이는 것뿐 아니라 오히려 모델 성능을 향상시키는 효과도 있음을 발견했다고.
- 즉 이 논문은 합성 데이터를 포함해 무작정 데이터 규모를 늘리기보다, 중복과 불필요한 정보를 제거(프루닝)함으로써 더 적은 데이터로도 고품질 코드 생성할 수 있다고.
Introduction:
- 합성 코드 생성 접근 방법으로 알려진 건 Self-Instrcut, Evol-Instruct, OSS-Instruct 등이 있다고 함.
- 근데 이러한 데이터 합성 기술은 훈련 비용을 증가시키고 많은 계산 자원을 요구하여 비용이 많이 드는 문제가 이씅ㅁ.
- 파인튜닝에 대한 백그라운드 이야기를 하자면 많고 품질이 좋은 데이터가 있으면 더 나은 성능을 달성할 수 있다는 건 밝혀진 사항임.
- 최근에는 더 효율적인 파인튜닝 기법(PEFT 와 같은) 것들이 알려졌는데, 약간의 데이터만 있더라도 인간의 선호에 맞추기에는 충분할 수 있다고 함.
- 여기서는 데이터 정제 기술에 대해서 다룸. 일반적으로는 데이터 정제 기술을 쓰는 것도 비용임. 계산이 많이 들어가니. 여기서는 이러한 문제도 어느정도 줄일 수 있다고 함. 클러스터링 + 차원 축소를 이용해서. 그리고 정제된 척도를 이용해서 선별한다고 함.
- 여기서 발견한 사항으로는 세부적인 제어 실험을 통해 클러스터링 알고리즘이 중요하며, 정제 척도의 중요성은 상대적으로 낮음을 발견했다고 한다.
- 차원 축소는 고차원 데이터 처리는 computationally expensive 크기 때문에 이를 해결하기 위해서 나온 기법임.
배경지식: 대표적인 차원 축소 기법 PCA(Principal Component Analysis):
- 차원 춗는 고차원 데이터를 더 낮은 차원으로 변환하는 기법을 말함.
- PCA 는 데이터를 중심화 (평균을 0으로) 만든 후, 분산이 가장 큰 주요소들 위주로 선택을 하는 기법임:
- 분산이 크다는 건 데이터가 많이 퍼져있다는 거고, 이게 중요한 차이를 내는 요소일 확률이 높기 때문임.
- 그 방향에 데이터의 중요한 패턴이나 특징이 있을 가능성이 높음
- 예로 데이터에 100개의 요소가 있다라고 한다면, PCA 를 이용해서 10개의 주요소를 뽑아내니 전체 분산의 95%를 차지한다면 아주 효과적인 걸꺼임.
배경지식 - 다양한 클러스터링 알고리즘 (HDBSCAN, KMeans, Agglomerative Clustering):
- HDBSCAN(Hierarchical Density-Based Spatial Clustering of Applications with Noise):
- 밀도 기반 클러스터링 알고리즘.
- 밀도의 정의:
- 특정 반경(ε) 내의 데이터 포인트 수
- 예: 반경 3 내에 포인트가 5개 이상 → 밀도가 높다고 판단
- 데이터의 밀도가 높은 영역을 클러스터로 식별하고, 밀도가 낮은 영역은 노이즈로 처리
- 밀도의 정의:
- DBSCAN의 개선된 버전으로, 계층적 클러스터링을 결합한 형태:
- 계층적 요소란 다양한 밀도 수준에서의 클러스터링을 한다는 걸 말함.
- Level 1 (높은 밀도): 매우 조밀한 클러스터들 발견
- Level 2 (중간 밀도): 더 큰 클러스터들로 병합
- Level 3 (낮은 밀도): 더 느슨하게 연결된 큰 클러스터들
- 이렇게 형성된 계층 구조를 트리(dendrogram)로 표현
- DBSCAN: 하나의 고정된 밀도 임계값을 사용했다고 함.
- 작동 원리:
- Step 1: 거리 계산
- 모든 포인트 쌍 간의 거리 계산
- mutual reachability distance 개념 사용
- 이건 각 포인트 p에 대해 core distance 계산하는 것부터 시작함.
- core_distance(p) = 거리를 정렬했을 때 mpts번째로 가까운 이웃까지의 거리
- 여기서 mpts 는 파라미터 변수임.
- mutual reachability distance 는 mrd(a,b) = max(core_distance(a), core_distance(b), distance(a,b)) 를 통해 계산됨.
- 밀도가 높으면 core_distance 는 낮게 나올거임. mutual reachability distance 는 이 중 최대값으로 결정하므로, 두 지점의 거리와 core_distance 를 비교해서 높은 값으로 결정될거임. 밀도가 낮다면 높은 값으로 mrd 가 결정되는거 반대로 밀도가 높다면 낮은 값으로 결정된다.
- Step 2: 최소 스패닝 트리 생성
- mrd 값으로 최소 스패닝 트리를 결정함.
- 최소 스패닝 트리는 그래프를 모두 연결했을 때 가중치의 합이 최소가 되도록 하는 트리를 말함.
- 최소합이 되도록 연결했는데 높은 가중치를 가지는 값은 밀도가 낮은 클러스터로 묶일 확률이 높고, 가중치가 낮은 값을 가지는 포인트들은 밀도가 높은 클러스터로 묶일 수 있을거임.
- 가중치가 큰 간선들을 순서대로 제거하면 클러스터로 구분을 시킬 수 있을 것.
- Step 3: 계층적 클러스터 추출
- 밀도 기반으로 클러스터 계층 구조 생성
- Step 4: 클러스터 추출
- 안정적인 클러스터 선택. 노이즈 포인트 식별 및 제거
- Step 1: 거리 계산
- 장점:
- 클러스터 수를 사전에 지정할 필요 없음
- 다양한 모양과 크기의 클러스터 발견 가능
- 노이즈에 강건함
- 밀도가 다른 클러스터도 잘 찾아냄
- 단점:
- 계산 복잡도가 높음 (O(n²))
- 메모리 사용량이 많음
- 논문에서 사용한 이유:
- 코드의 구문적 대표성을 찾는데 적합.
- 노이즈(저품질 데이터)를 자동으로 제거
- 클러스터 수를 자동으로 결정할 수 있다는 점을 장점으로 활용
- 밀도 기반 클러스터링 알고리즘.
- KMeans:
- 데이터를 K개의 그룹(클러스터)으로 나누는 알고리즘
- 각 클러스터는 하나의 중심점(centroid)을 가짐
- 각 데이터 포인트는 가장 가까운 중심점의 클러스터에 할당됨
- 계속 데이터를 배치하고, 중심점을 새로 계산하는 식으로 동작함.
- 작동 원리:
- 1단계: 초기화
- K개의 중심점(centroid)을 무작위로 데이터 공간에 배치
- 2단계: 할당(Assignment)
- 각 데이터 포인트에서 모든 중심점까지의 거리를 계산
- 가장 가까운 중심점의 클러스터에 해당 포인트를 할당
- 3단계: 업데이트(Update)
- 각 클러스터에 속한 포인트들의 평균 위치를 계산
- 이 평균 위치를 새로운 중심점으로 설정. 이런식으로 점점 수렴하게 되는거임.
- 4단계: 반복
- 2~3 단계를 반복
- 반복할수록 좀 더 정확한 중심점이 계산될 것.
- 1단계: 초기화
- 장점:
- 구현이 간단하고 이해하기 쉬움
- 대규모 데이터셋에서도 효율적으로 작동:
- 시간 복잡도와 관련이 있음.
- n = 데이터 포인트 수, k = 클러스터 수, i = 반복 횟수 라고 할 때 O(n*k*i) 가 시간 복잡도임.
- 단점:
- K값을 사전에 지정해야 함 (이게 가장 큰 단점. 정적임. 몇개로 분류될지 모르는데)
- 반복 횟수가 적다면 운에따라 성능이 좀 결정됨.
- 논문에서 활용한 이유:
- 대규모 데이터 셋에 적합 및 확장성 높음.
- Agglomerative Clustering(병합적 계층 클러스터링):
- 상향식(bottom-up) 계층적 클러스터링 방법.
- 각 포인트를 개별 클러스터로 시작해서 점진적으로 병합
- 트리 형태의 계층 구조(덴드로그램)를 생성 (= 덴드로그램을 통해 클러스터 형성 과정을 시각적으로 이해 가능)
- 작동 원리:
- (1) 각 데이터 포인트를 독립된 클러스터로 초기화
- (2) 클러스터의 개수가 내가 바라는 클러스터 수가 많다면 클러스터 수를 합치기 시작함. (아니면 distance_threshold 값을 지정해서 이 거리 값 내에 있는 건 합칠 수 있음)
- (3) 가장 가까운 두 클러스터를 찾아서 병합하는 식으로
- 클러스터 간 거리 계산 방법(linkage) 은 다양하게 있음:
- Single linkage: 두 클러스터의 가장 가까운 포인트 간 거리
- Complete linkage: 두 클러스터의 가장 먼 포인트 간 거리
- Average linkage: 모든 포인트 쌍의 평균 거리
- Ward's method: 클러스터 내 분산 증가를 최소화
- 장점:
- 클러스터의 계층 구조를 파악 가능
- 클러스터 수를 사전에 지정할 필요 없음 (distance threshold 값을 지정한다면)
- 단점:
- 계산 복잡도가 높음 O(n^3)
- 큰 데이터셋에서는 메모리 사용량이 많음
- 논문에서 사용한 이유:
- 중첩된(nested) 클러스터를 만들 수 있음: 이는 클러스터 안에 또 다른 클러스터가 포함될 수 있다는 의미로 다른 계층별로 유사성 기준이 다를 수 있다는 거임. 이런 세밀함이 데이터셋의 품질을 유지하는데 도움이 된다는 것.
- 큰 범주의 유사성도 보존하지만, 세부적인 유사성도 보존. 결과적으로 데이터셋의 다양한 특성을 잘 보존할 수 있다.
배경지식 - 차원의 저주:
- 데이터의 차원이 증가할수록 발생하는 다양한 문제들을 총칭
- 동일한 수의 데이터 포인트도 차원이 높아지면 공간이 희소해짐, 고차원에서는 모든 포인트 쌍의 거리가 비슷해짐 (예: 1000차원에서는 대부분의 포인트가 서로 "멀다"고 판단됨)
- 차원이 증가할수록 의미 있는 분석을 위해 필요한 데이터가 기하급수적으로 증가
Methodology:
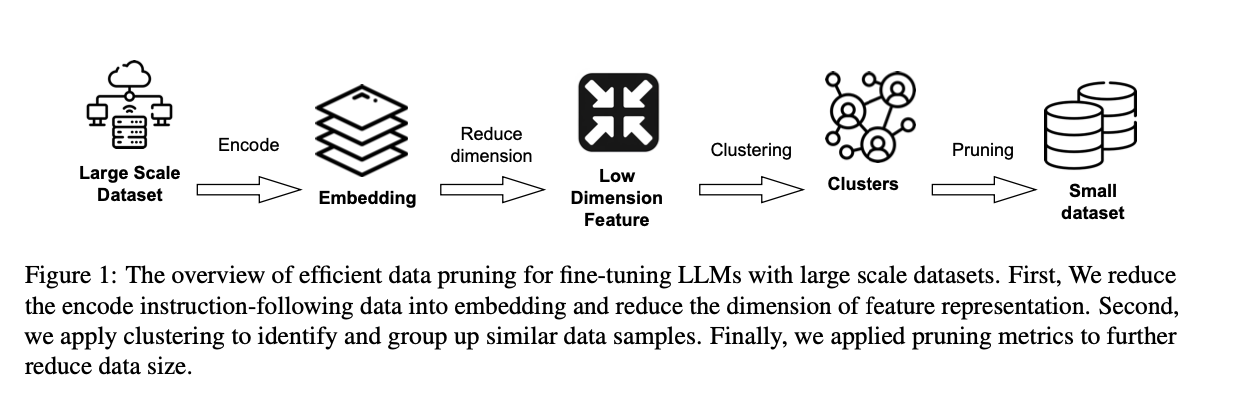
- 이 논문의 목표는 높은 품질의 대표적인 데이터 샘플을 선택하여 이들을 훈련함으로써 전체 데이터 세트를 사용할 때와 동등하거나 더 나은 성능을 얻는 것임
- 대규모 데이터세트로 LLM을 효과적으로 미세 조정하기 위한 효율적인 데이터 정제 개요는 다음 그링메 있음.
- 먼저, 임베딩 모델을 사용하여 지시-코드 쌍을 벡터 표현으로 투영, 다음, 계산 복잡성을 줄이기 위해 특징 표현의 차원을 낮추고, 클러스터링을 적용하여 유사한 데이터 샘플들을 식별하고 그룹화.
- 마지막으로, 데이터 크기를 줄이기 위해 정제 지표를 적용합니다. 자세한 알고리즘은 Algorithm 1에 나와 있습니다.
Algorithm 1 Data Pruning Algorithm:

- 1 초기화 단계: 임베딩 모델과 압축 비율을 초기화합니다.
- 2 임베딩 적용: 주성분 분석(PCA)을 사용하여 데이터의 차원을 축소한 후, 이를 이용해 임베딩을 투영합니다.
- 3 클러스터링: 차원이 축소된 데이터(X)를 사용하여 클러스터링 알고리즘을 적용합니다. 이 단계에서는 유사한 데이터 샘플을 그룹화합니다.
- 4 클러스터 처리: 각 클러스터별로 다음의 단계를 수행합니다.
- 정제 점수 계산: 각 클러스터 내의 항목들을 대상으로 정제 지표를 사용하여 점수를 계산합니다.
- 랜덤 선택: 계산된 점수를 기반으로 항목들을 무작위로 선택합니다. 점수가 높을수록 선택될 확률이 높아집니다.
- 클러스터 업데이트 및 선택 모음에 추가: 선택된 항목들을 해당 클러스터와 최종 선택 목록에 업데이트합니다.
- 결과 출력: 최종적으로 선택된 데이터 샘플을 출력합니다.
Dimension Reduction:
- 차원 축소 과정은 각 지시-코드 쌍을 벡터 표현으로 변환하는 과정을 통해 클러스터링 및 데이터 정제 지표의 계산 효율성을 높이는게 목표
- 계산 복잡성을 줄이기 위해 우리는 주성분 분석(PCA)을 사용하여 벡터 표현의 차원을 축소함.
- LLM에서 추출한 표현은 종종 천 개 이상의 차원을 가지기 때문에, 차원 축소는 필수적이라고 한다. 또한 높은 차원 공간에서 여러 커널 방법을 사용하는 것 (클러스터의 밀도를 추정해서 프루닝(Pruning) 것도 차원의 저주를 받기 떄문에 필요하다고 함.
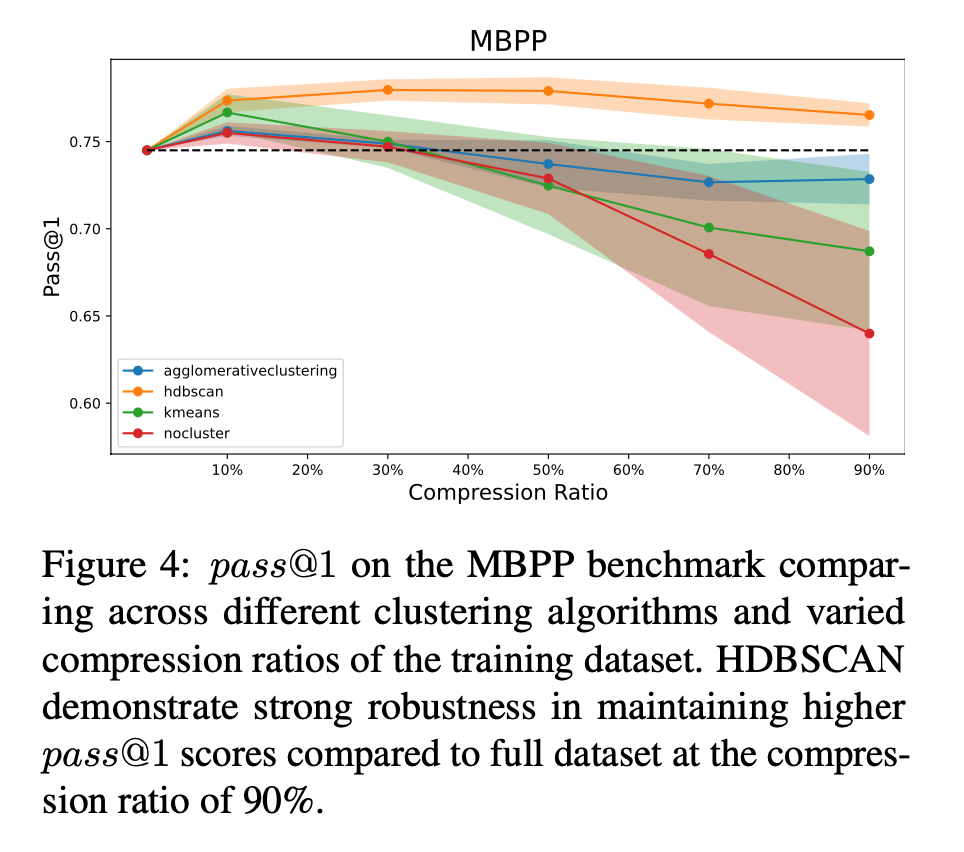
- 차원 축소를 하면 성능 지표가 MBPP (pass@1) 에서는 0.6% 감소, HumanEval 에서는 4.3% 감소한다고 함. 그러나 클러스터링 알고리즘에서는 KMeans 기준으로 12배 빨라지고, HDBSCAN 도 4시간 이내에 완료될 수 있다고 함.
Clustering:
- 클러스터링은 유사한 지시-코드 쌍을 그룹화하는 중요한 단계로, 다양한 대표 샘플을 선택하는 데 도움을 줌.
- 클러스터링을 수행하기 전에, 각 특징이 거리 계산에 동등하게 기여하도록 벡터 표현을 정규화 한다고 함.
- scikit-learn의 클러스터링 알고리즘들은 기본적으로 정규화하지 않기 떄문에 이게 필요함.
- 스케일이 큰 특징이 거리 계산에 과도한 영향을 미칠 수 있다.
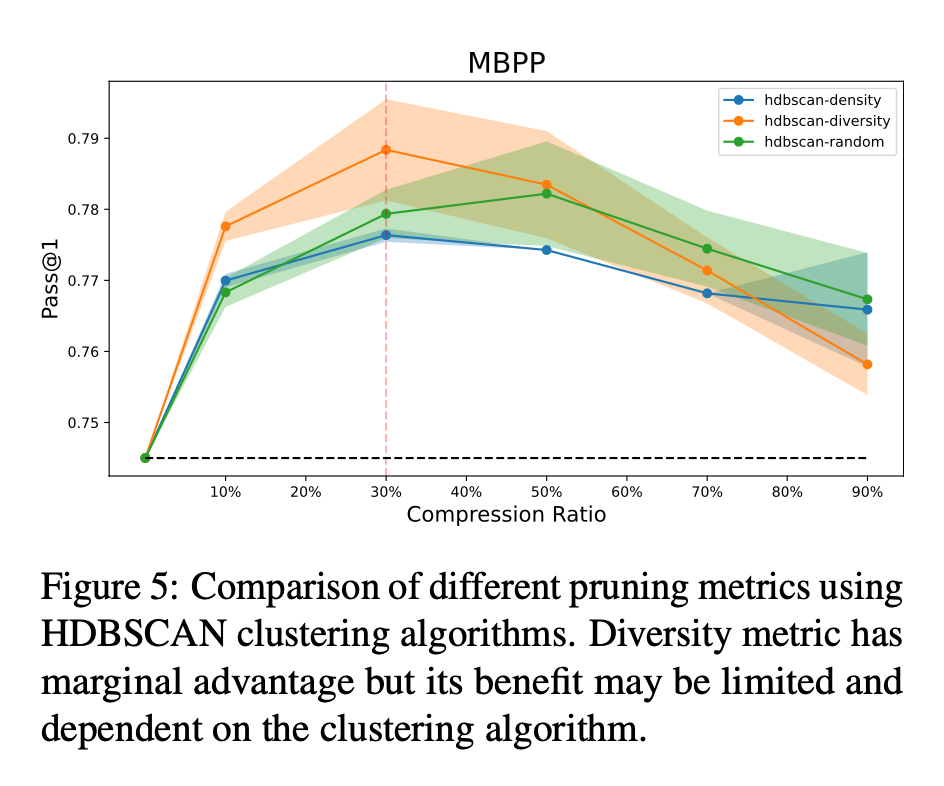
Pruning Metrics:
- 다양성 지표르 계산하기 위해 Pruning Metric 을 씀:
- Diversity Metric:
- di = min(x∈K{xi}) dist(xi, x), di는 샘플 xi의 다양성 점수, K는 클러스터 내의 선택된 쿼리 세트, dist는 거리 함수
- 각 포인트에 대해 가장 가까운 선택된 포인트와의 거리를 계산. 이 계산 값이 크다는 건 거리가 많이 떨어져있다는 것으로 다양성 지표에서 높은 점수를 받음.
- Density Metric:
- 커널 밀도 추정(KDE)을 사용하여 특징 공간에서 샘플의 밀도를 측정함.
- 높은 밀도 값을 가진 다는 건 다양성이 떨이진다는 것으로 해석함.
- 반면 낮은 밀도 값을 가진 포인트는 다양성이 높다고 해석
- 이렇게 점수를 얻은 후, 이 점수 보다 높은 값을 클러스터에서 랜덤 선택하는 식으로 정제를 함.
- Pruning Metrics 으로는 Random, Diversity, Density 를 합쳐서 쓰는게 아님. 각각 써봤다고
Implementation Details:
- 모든 클러스터링 및 커널 밀도 추정 파라미터는 sklearn의 기본 설정을 따랐다고 함.
- 클러스터의 최적 수를 선택해야 하는 알고리즘(KMeans와 같은)의 경우, Elbow 방법을 사용하여 추가 클러스터를 추가해도 설명되는 분산이 크게 개선되지 않는 지점을 찾는 식으로 사용했다고 함:
- Elbow method는 K-means 클러스터링에서 적절한 K(클러스터 수)를 찾는 방법이라고 함.
- 다양한 K값에 대해 클러스터 내 분산(inertia 또는 WCSS: Within-Cluster Sum of Squares)을 계산.
- 이 분산의 팔꿈치 값 (분산이 크게 떨어지는 값으로 이후부터는 이제 잘 안떨어짐) 을 최적의 K 값으로 판단하는 것.
- 분산은 클러스터내의 응집도를 나타내는 값으로, 분산이 크다는건 클러스터내의 데이터가 안뭉쳐져있다, 위확감이 든다는 것을 나타내며, 데이터의 특성을 잘 나타내지 못함.
- Elbow method는 K-means 클러스터링에서 적절한 K(클러스터 수)를 찾는 방법이라고 함.
- 정제 지표에 대해서는 Gaussian 커널 대역폭을 결정하기 위해 Scott's Rule을 적용하였고, 다양성 지표를 위해 데이터셋의 10%를 무작위로 선택하여 쿼리 세트((K))로 사용했다고 한다.
- 실험에서는 PCA 차원 축소를 벤치마크 데이터셋에 맞춘 후, 지시 데이터에 투영을 적용했다고 함
- 임베딩은 OpenAI의 text-embedding-ada-002 임베딩 모델을 사용하여 데이터를 인코딩했다고 함. 코드만 임베딩 할건지, 지시문까지 임베딩할건지 성능 비교를 통해 판단했는데 이 케이스는 지시문까지 합치는게 더 나았다고 함.
결과 - 클러스터링 알고리즘 성능과 Pruning Metric: