Undirected Grapth

Undirected Graph

Graph 의 정의란?

Set of vertices connected pairwise by edges

 

 

Vertex 는 Node 를 말하고, Edge 는 Vertex 들이 연결된 것을 말한다.

 

 

대표적인 실생활의 Graph 는 지하철 노선도가 있다:

 

Graph terminology 정리:

Path:

• Vertex 들이 연결된 길을 말한다.

Cycle:

• Path 를 따라 갔을 때 첫 번째 Vertex 와 Last Vertex 가 동일한 경우를 말한다.

 

대표적인 용어들을 포함한 이미지는 다음과 같다: 

 

Graph 와 관련된 일반적인 문제들:

Path:

• 두 Vertex 사이에 Path 가 있는지?

Shortest path:

• 시작점 Vertex 에서 도착점 Vertex 로 가는 최소 비용이 드는 Path 는 무엇인지? (갈 수 있는 방법이 많을 것이고, 각 방법마다 비용이 다를 것이다)

Cycle:

• Grpah 에 Cycle 이 있는지?

Euler tour:

• Graph 에서 Euler tour 가 있는지?
• (Euler tour 는 Graph 에 있는 모든 Edge 들을 한번만 방문해서 처음으로 돌아오는 것을 말한다.)

Hamilton tour:

• Graph 에서 Hamilton tour 가 있는지?
• Hamilton tour 는 Graph 에 있는 모든 Vertex 를 한번만 방문해서 처음으로 돌아오는 것을 말한다.

Connectivity:

• Graph 에서 모든 Vertex 가 연결될 수 있는가?

MST (Minimum Spanning Tree):

• Graph 에서 모든 Vertex 를 연결시킬 때 최소한의 비용으로 만드는 방법은 무엇인가?

Biconnectivity.

• Graph 에서 어떤 Vertex 를 제거해도 Graph 가 Connectivity 속성을 가질 수 있는가?
• Graph 에서 어떤 Edge 를 제거해도 Graph 가 Connectivity 속성을 가질 수 있는가?

Planarity:

• Graph 를 평면에 그렸을 때 어떠한 Edge 도 서로 교차 (Crossing) 되지 않게 그릴 수 있는가?

Graph isomorphism:

• 두 그래프의 adjacency lists 를 봤을 때 동일한 그래프인지 판단할 수 있는가?

 

Euler tour 는 만족하지만 Hamilton tour 는 만족하지 않는 경우 (= 모든 Vertex 를 돌고도, 여분의 Edge 가 있어서 추가로 왔다갔다 하는 경우에는 HHamilton tour 를 만족시키지 못한다.)

• 아래의 예시에서는 오일러 투어의 경로: A -> B -> F -> E -> C -> A -> D -> B -> E -> F -> A
• 그래프에서 누락된 부분이 있다. ( E -> B 와 F -> A )
  

  

 

Hamilton tour 는 만족하지만 Euler tour 는 만족하지 않는 경우를 생각해보는 건 쉽다.

 

모든 Vertex 를 방문하고 돌아와도 여분의 Edge 만 있으면 Euler tour 는 만족하지 못한다.

 

 

Graph API

기본적인 API 들은 다음과 같다:

• Graph(int V):
  • V 개의 Vertex 를 가진 Graph 생성
• void addEdge(int v, int w):
  • Vertex v 에서 w 로의 Edge 를 추가
• Iterable<Integer> adj(Int v):
  • Vertex V 에서 연결된 Vertex 들을 구하는 것. (= Edge 를 말하는 것이기도 하다.) 
• int V():
  • 이 Graph 에서 Vertex 의 수
• int E():
  • 이 Graph 에서 Edge 의 수

 

Typical Grpah-proceesing code

먼저 Degree 에 대해서 정의하자면 Degree 는 해당 Vertex 에 연결된 Edge 의 수를 말한다.

 

아래의 이미지는 Graph 에서 사용하는 Degree 와 관련된 코드이다.

• averageDegree() 는 하나의 Vertex 당 평균적으로 몇 개의 Edge 와 연결되어 있는지를 설명하는 메소드이다.
• 하나의 Edge 는 2개의 Vertex 가 공유하고 있는 형태니까 averageDegree() 를 계산할 때 전체 Edge * 2 를 해주는 것이다.

 

Graph Representation

Graph 를 표현하는 방법은 두 가지가 있다:

• Matrix 를 이용하는 것
• Adjacency List 를 이용하는 것

 

Adjacency-matrix graph representation

이미지로 보자:

• 두 Vertex 사이의 Edge 를 표현할 때 adj[v][w] 로 표현한다.
• Edge 는 두 Vertex 가 공유하는 것이다. 그래서 Vertex v 와 w 사이의 Edge 를 표현하려면 adj[v][w] = true 이면서 adj[w][v] = true 이어야한다.

 

Adjacency-list graph representation

이미지로 보자:

• 해당 Vertex 마다 List 형식으로 Edge 들을 가지고 있다.
  

  

 

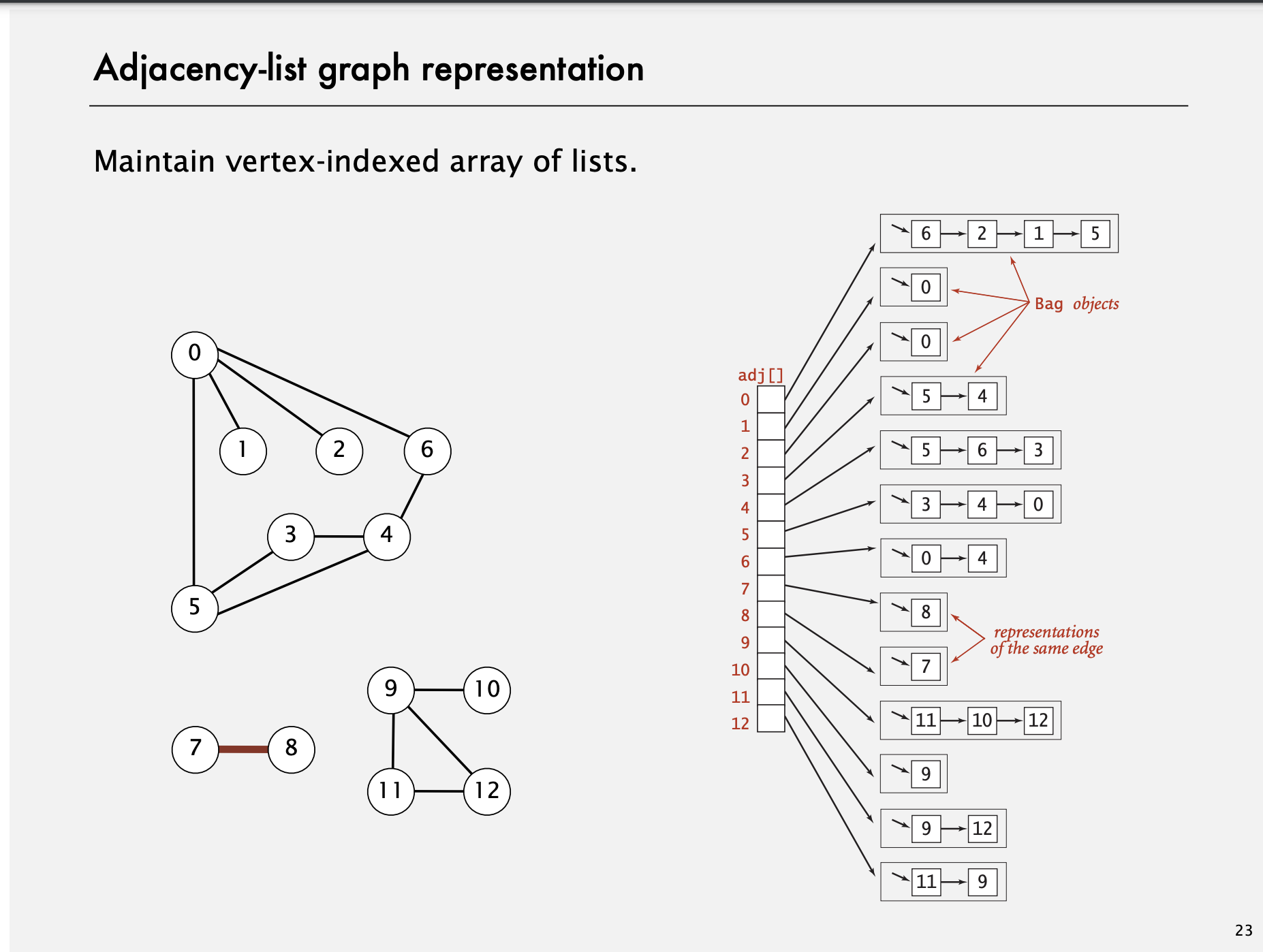
자바 코드로 보면 다음과 같다:

 

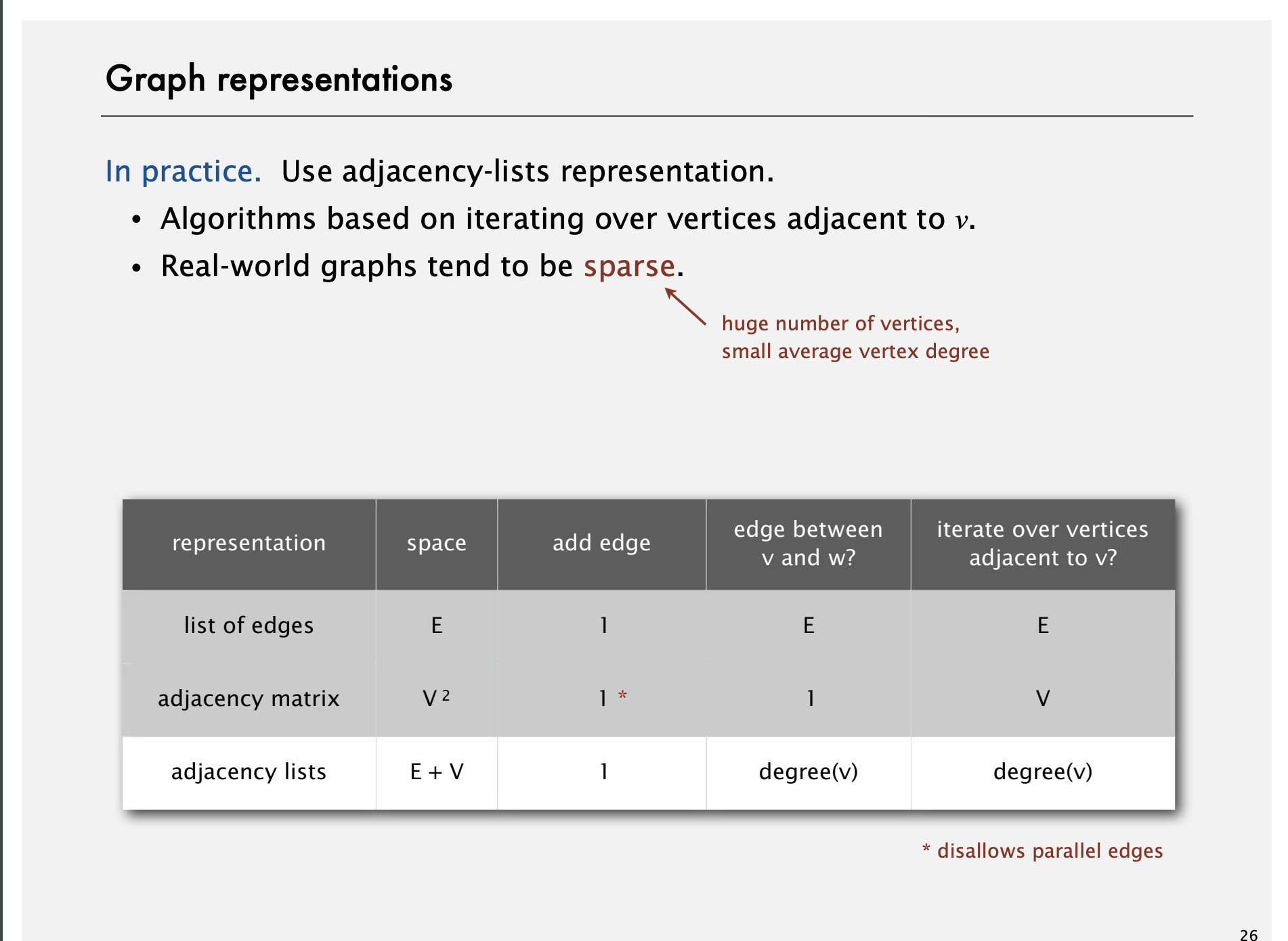
Adjacency-matrix VS Adjacency-list

Adjacency-matrix 단점:

• Vertex * Vertex 만큼 배열로 관리하기 때문에 메모리 공간을 더 많이 쓴다. Real World 에서의 Graph 는 대부분 Sparse 하기 때문에 대부분의 상황에서 Matrix 는 적합하지 않을 것이다.
• Vertex 가 가지고 있는 Edge 를 순회하는 것도 Matrix 는 전체 Vertex 만큼 다 순회해야하므로 Adjacency List 보다 느리다.

 

Adjacency-matrix 가 더 나은 점:

• 두 Vertex 가 연결되어 있는지 파악하는 것은 O(1) 으로 Adjacency List 보다 더 빠르다.

 

DFS

Graph 에 있는 시작점 Vertex S 로 부터의 Graph 에 있는 모든 Vertex 를 탐색하는 방법을 다룬다. 

 

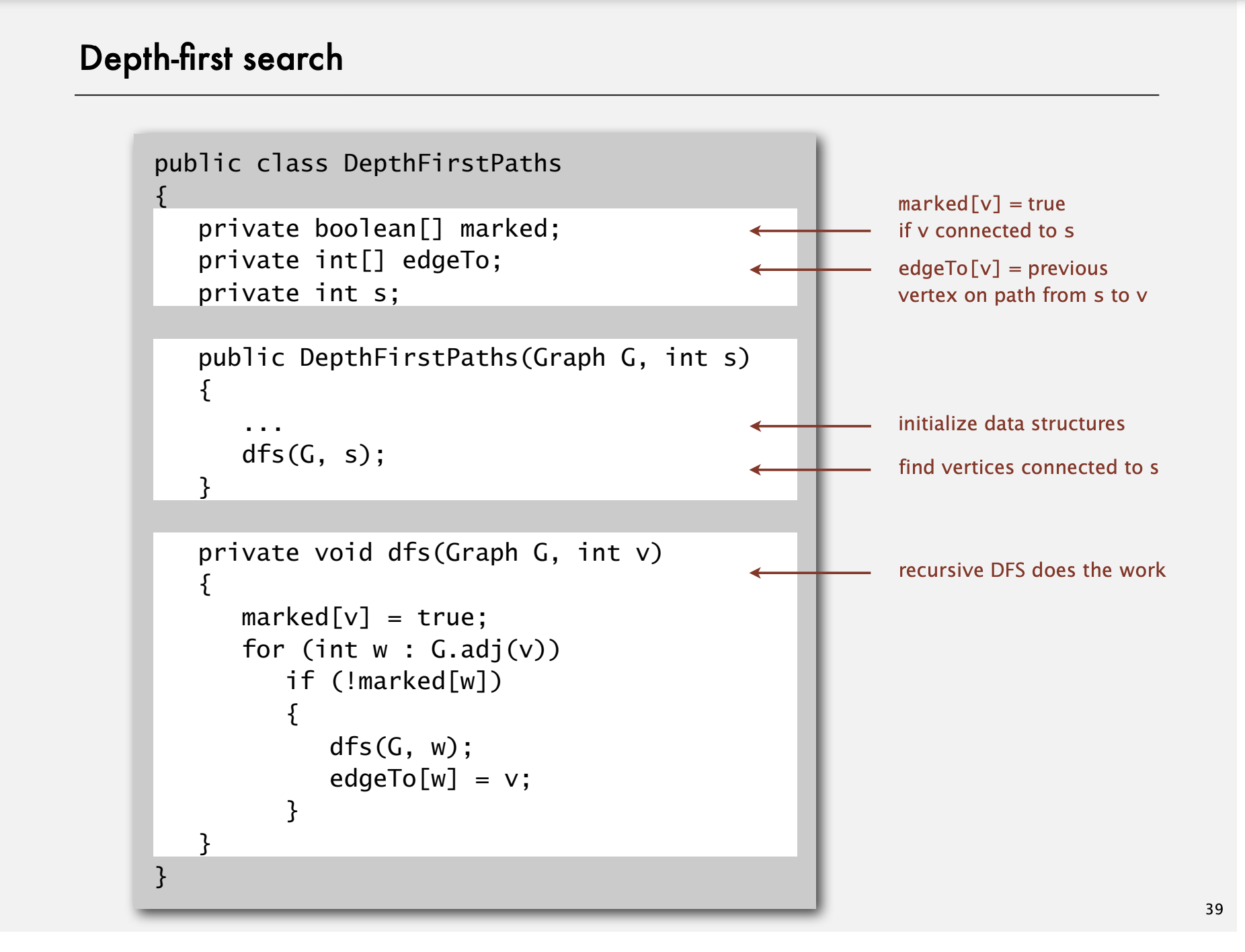
아래 이미지의 Data Structure 에 주목하자:

• boolean[] marked 를 통해서 방문한 점은 또 다시 방문하지 않도록 한다.
• int[] edgeTo 를 통해서 DFS 의 Path 를 추적할 수 있다. edgeTo[w] = v 는 V -> W 를 말한다. 즉 도착점에서부터 자신이 온 길을 추적하는게 가능하다.

 

 

Graph DFS 를 Java 로 구현하면 다음과 같을 것이다:

 

DFS 검색으로 발견할 수 있는 명제들:

• Graph 의 Vertex S 부터 시작해서 DFS 검색을 헀을 때, Vertex W 가 marked 되어있다면 S 와 W 는 연결되어 있는 것이다. 역도 가능하다. 연결되어 있다면 marked 되었을 것이다.
• 만약 Graph 의 Vertex S 부터 시작해서 DFS 검색을 헀을 때, Vertex W 가 unmarked 되어있다면 두 Vertex S 와 W 는 서로 연결되어 있지 않는 것이다.
• Graph DFS 에서 Vertex 의 방문은 오로지 한 번만 한다

 

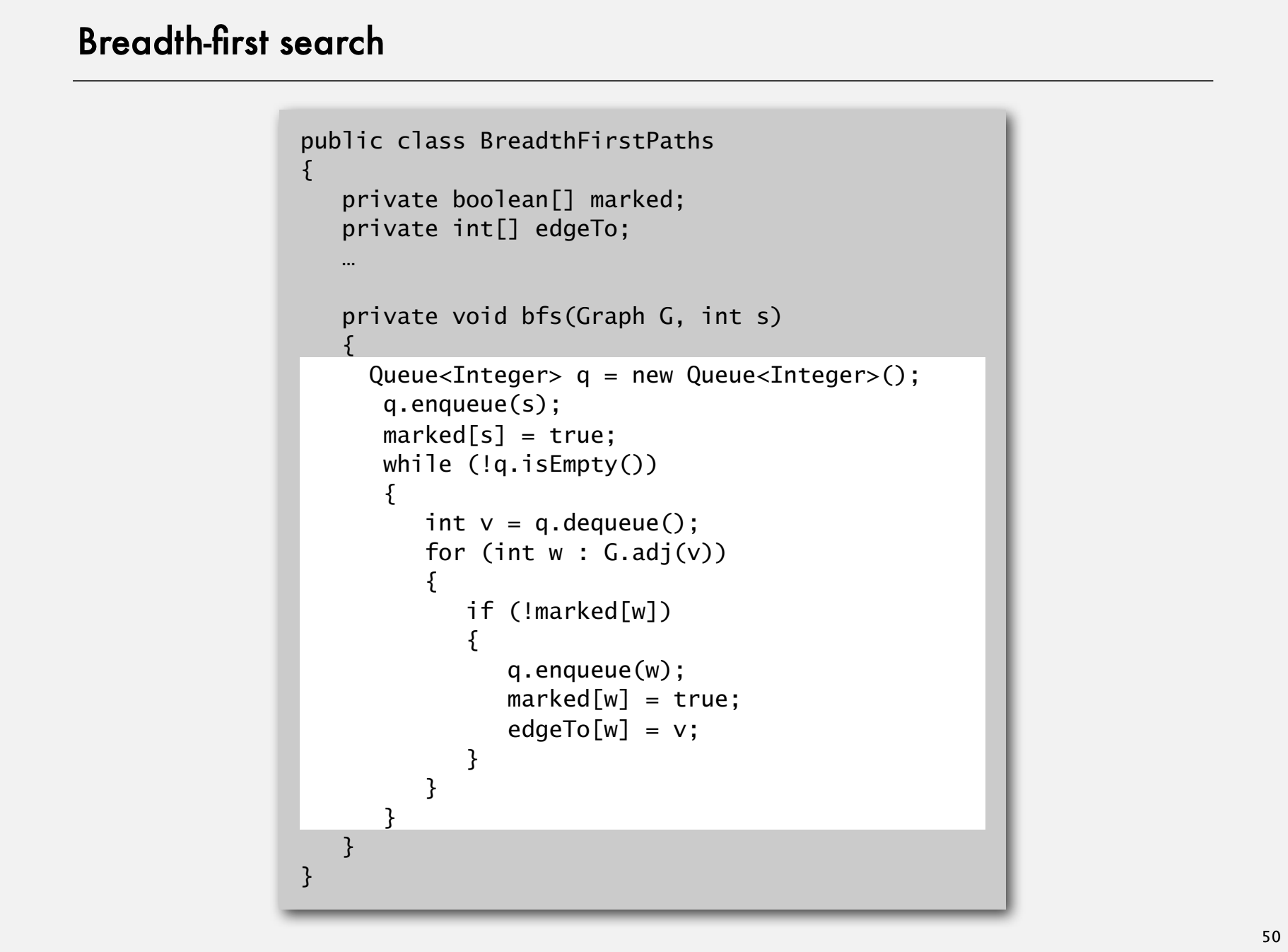
BFS

BFS 를 이용해서 Graph 를 탐색하는 방법의 코드는 다음과 같다:

 

BFS 검색으로 발견할 수 있는 명제들:

• Vertex S 에서 Vertex W 까지의 거리는 최소한의 edge 를 타서 검색이 된다. (= Shortest Path)

 

Connected Components

Graph 가 주어졌을 때 모든 Vertex 가 연결되어 있지는 않을 것이다.

 

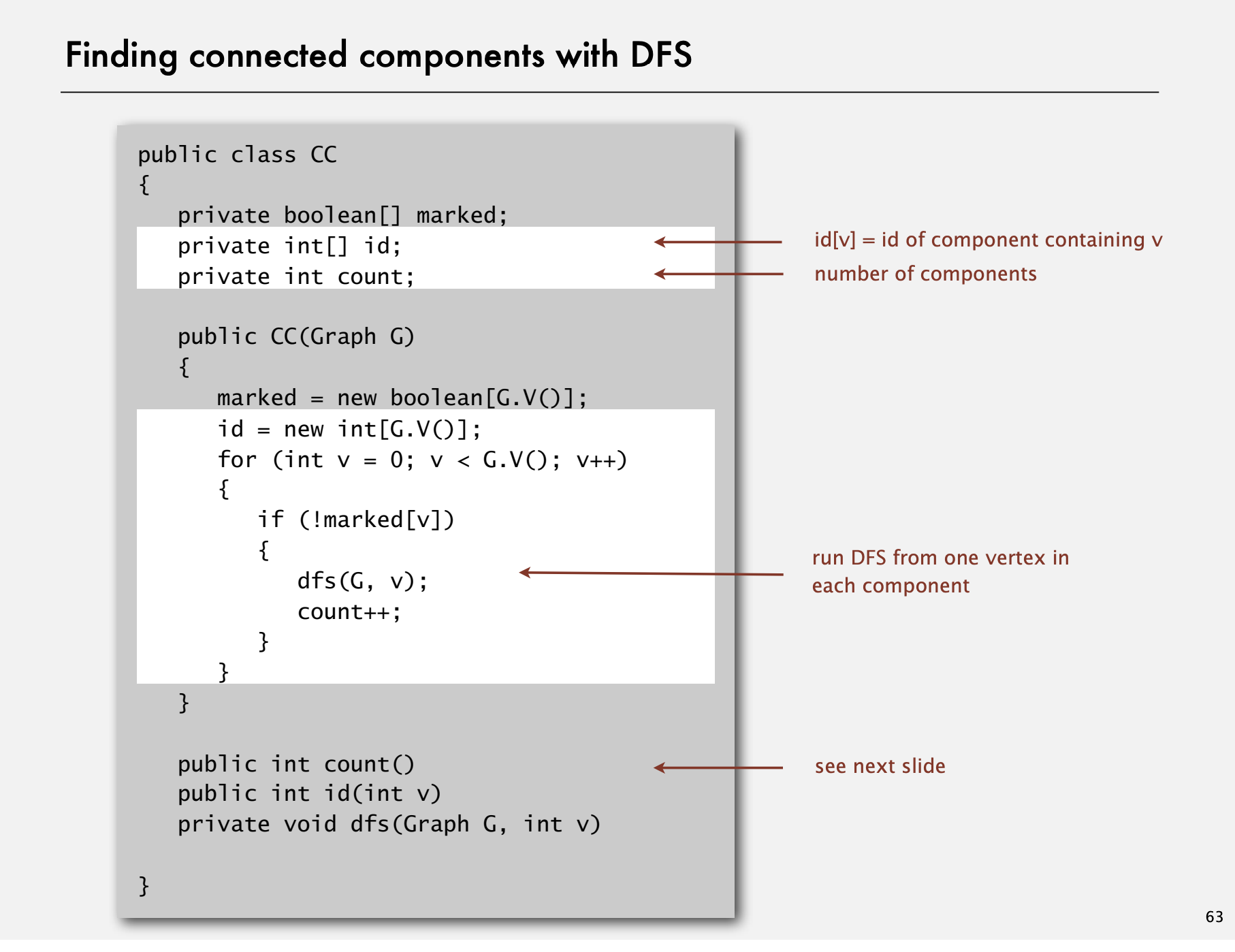
여기서는 CC 라는 클래스를 만들어서 Vertex v 와 w 가 서로 연결되어 있는지 판단하는 방법을 작성해보겠다.

 

 

Vertex v 와 w 가 서로 연결되어 있는지 판단하는 방법은 다음과 같다:

• DFS 를 통해 검색 된 Vertex 들은 서로 연결되어 있다는 사실을 알 수 있다.
• DFS 로 검색되는 Vertex 들에게 서로 연결되어 있음을 알려주는 식별 값을 넣어주는 것으로 구현할 수 있다.

 

References:

https://www.coursera.org/learn/algorithms-part2?action=enroll